4 Buckingham Pi theorem
As suggested in the last section, if there are more than 4 variables in the problem, and only 3 dimensional
quantities (M, L, T), then we cannot find a unique relation between the variables. The best we can hope for is
to find dimensionless groups of variables, usually just referred to as dimensionless groups, on which the
problem depends. In fact, this is quite a good approach, for reasons that will be discussed in the next
section.
Buckingham Pi is a procedure for determining dimensionless groups from the variables in the
problem.
4.1 The Rules
Let us assume that there are n = 3 dimensional quantities to consider - mass, length and time. The problem
involves m = 6 variables, denoted A . . . F. In general we can derive m - n dimensionless groups, often denoted
 1,
1,  2..., using the following procedure
2..., using the following procedure
- Write down the dimensions for all variables A . . . F
- Select n of the variables - say A, B, C. These are called the repeating variables, and will appear in all the
 terms. Note that there are certain restrictions on our choice :
terms. Note that there are certain restrictions on our choice :
- None of the repeating variables can be dimensionless
- No two repeating variables can have the same overall dimension. For instance, D, the pipe
diameter, and r, the roughness height, both have dimension of L, and so cannot both be used
as repeating variables.
- Select one other variable - say D. Some combination of A, B, C, D is dimensionless, and forms the first
 term or dimensionless group. We can find the combination by dimensional analysis, by writing the
group in the form
term or dimensionless group. We can find the combination by dimensional analysis, by writing the
group in the form
![a b c d a b c d
TT1 = A B C D , so [ ] = [A] [B] [C] [D]](../DimensionalAnalysis/dimensionalLecture30x.gif) Equating coefficients gives 3 equations for 4 unknowns, so we can express all the coefficients in terms of
just one.
Equating coefficients gives 3 equations for 4 unknowns, so we can express all the coefficients in terms of
just one.
- Repeat this procedure with the repeating variables and the next variable, so use A, B, C, E. Continue
until no variables are left.
- Having worked out all the dimensionless groups, the relationship between the variables can be expressed
as a relationship between the various groups. Typically we can write this as one group (for example
 1 as
a function of the others
1 as
a function of the others
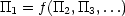
4.2 Worked example
This is probably best illustrated by a worked example. The head loss in a horizontal pipe in turbulent
flow is related to the pressure drop 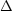 p, and is a measure of the resistance to flow in the pipe. It
depends on the diameter of the pipe D, the viscosity
p, and is a measure of the resistance to flow in the pipe. It
depends on the diameter of the pipe D, the viscosity 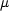 and density
and density 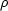 , the length of the pipe l, the
velocity of the flow v and the surface roughness
, the length of the pipe l, the
velocity of the flow v and the surface roughness 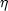 . We start by listing the dimensions of these
parameters
. We start by listing the dimensions of these
parameters
| D | [L] |
| v | [LT-1] |
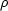 | [ML-3] |
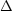 p p | [ML-1T-2] |
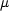 | [ML-1T-1] |
| l | [L] |
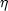 | [ ] |
| |
We will choose D, v and 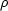 as repeating variables. Our first dimensionless group involves
as repeating variables. Our first dimensionless group involves 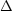 p, in the
form
p, in the
form
![a b c d a - 1b -3c -1 -2 d
D v r Dp , so [ ] = [L] [LT ] [M L ][M L T ]](../DimensionalAnalysis/dimensionalLecture32x.gif) This gives the relations
This gives the relations
| 0 | = c + d | |
|
| 0 | = -b - 2d | |
|
| 0 | = a + b - 3c - d | | |
equating coefficients of M, T and L respectively. Writing them all in terms of d,
| c | = -d | |
|
| b | = -2d | |
|
| 0 | = a - 2d + 3d - d 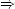 a = 0 a = 0 | | |
Resubstituting
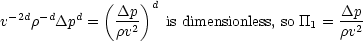
We can repeat the process with 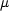 to get the second dimensionless group :
to get the second dimensionless group :
![Davbrcmd, so [] = [L]a[LT-1]b[M L- 3]c[M L -1T-1]d](../DimensionalAnalysis/dimensionalLecture34x.gif) Equating coefficients
Equating coefficients
| 0 | = c + d | |
|
| 0 | = -b - d | |
|
| 0 | = a + b - 3c - d | | |
Solving again in terms of d gives c = -d, b = -d and a = -d, thus
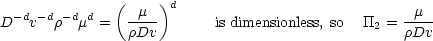 In fact, we recognise this group as the Reynolds number, written upside down, so
In fact, we recognise this group as the Reynolds number, written upside down, so
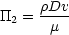
The next dimensionless group will involve l with dimension L. However one of the repeating variables is the
diameter D, and so the ratio of the two is already dimensionless. So the next dimensionless group
is
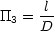 Finally,
Finally, 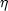 is already dimensionless anyway, being the ratio of the height of the roughness to the pipe diameter
D. so
is already dimensionless anyway, being the ratio of the height of the roughness to the pipe diameter
D. so
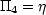
From this analysis we have successfully determined that the turbulent flow in a roughened pipe depends on
a head loss parameter
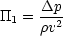 together with the Reynolds number, the ratio of the pipe length to diameter, and the surface roughness
coefficient. We can write this relation as a relation between the groups
together with the Reynolds number, the ratio of the pipe length to diameter, and the surface roughness
coefficient. We can write this relation as a relation between the groups
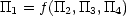 or in full
or in full
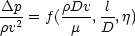
This is as far as we can go using dimensional analysis. Experiment however shows that the pressure drop
depends linearly on the length of the pipe, so we can make this relation explicit :
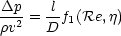 We can rearange this a little further, rewriting it as
We can rearange this a little further, rewriting it as
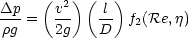 which is of course the Darcy equation for head loss in a pipe.
which is of course the Darcy equation for head loss in a pipe.
4.3 Helpful hints
There are a number of helpful short cuts that can simplify matters :
- If a quantity is dimensionless, it is a
 term already
term already
- If any two variables have the same dimensions, their ratio will be a
 term
term
- In the final expression, the dimensionless groups can appear in any functional form. In particular,
the expression may depend on
 -1 as easilly as on
-1 as easilly as on  , so any dimensionless group can be inverted
if that is more convenient.
, so any dimensionless group can be inverted
if that is more convenient.
- Any
 term may be expressed in terms of the others.
term may be expressed in terms of the others.
All of these short cuts were used in the previous example.
![]() 1,
1, ![]() 2..., using the following procedure
2..., using the following procedure
![]() p, and is a measure of the resistance to flow in the pipe. It
depends on the diameter of the pipe D, the viscosity
p, and is a measure of the resistance to flow in the pipe. It
depends on the diameter of the pipe D, the viscosity ![]() and density
and density ![]() , the length of the pipe l, the
velocity of the flow v and the surface roughness
, the length of the pipe l, the
velocity of the flow v and the surface roughness ![]() . We start by listing the dimensions of these
parameters
. We start by listing the dimensions of these
parameters
![]() as repeating variables. Our first dimensionless group involves
as repeating variables. Our first dimensionless group involves ![]() p, in the
form
p, in the
form
![]() to get the second dimensionless group :
to get the second dimensionless group :