3 Determining equations
Let us suppose that we want to work out how the time period t for a pendulum depends on its length l and the
accelleration due to gravity g. Our principle, that each term in an equation has to have the same dimensions,
can be used to good effect. The time period t has dimensions [T], so if we write this as some function of l and
g
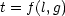 then f has to have these dimensions as well. If l and g are the only other variables in the problem, then we
need to find some combination of the two which has dimensions [T]. Since the dimensions of l are [L], and the
dimensions of g (an accelleration) are [LT-2], then
then f has to have these dimensions as well. If l and g are the only other variables in the problem, then we
need to find some combination of the two which has dimensions [T]. Since the dimensions of l are [L], and the
dimensions of g (an accelleration) are [LT-2], then
![l has dimensions [T 2]
g](../DimensionalAnalysis/dimensionalLecture11x.gif) This suggests that the time period is given by
This suggests that the time period is given by
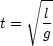 But wait a minute! The time period could also be given by
But wait a minute! The time period could also be given by
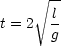 which is still dimensionally correct, since 2 is a pure number (no dimensions). In fact we could
multiply the rhs by any dimensionless number, so from considering dimensions we can conclude
that
which is still dimensionally correct, since 2 is a pure number (no dimensions). In fact we could
multiply the rhs by any dimensionless number, so from considering dimensions we can conclude
that
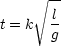 with k some dimensionless constant whose value has to be determined in some other way, generally
experimentally. In this case experiment shows that k = 2
with k some dimensionless constant whose value has to be determined in some other way, generally
experimentally. In this case experiment shows that k = 2 .
.
In this case, we could work out the relationship easilly from the dimensions of the variables. However
the relationship is not always this straightforward, and so we need a general technique for doing
this.
3.1 General approach
Now : the details. This approach works if we want to determine how a particular parameter in the
problem depends on 3 other parameters. For example, suppose we want to work out how the flow Q
of an ideal fluid through a hole of diameter D depends on the pressure difference 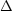 p. It seems
plausible that Q might also depend on the density of the fluid
p. It seems
plausible that Q might also depend on the density of the fluid 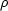 , so we look for a relationship of the
form
, so we look for a relationship of the
form
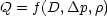 Specifically, our function f(...) should look like this
Specifically, our function f(...) should look like this
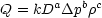 | (1) |
Here a, b, c are exponents whose form we want to determine. We can start by writing down the dimensions for
each of these quantities :
| [Q] | [L3T-1] |
| [D] | [L] |
[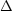 p] p] | [ML-1T-2] |
[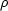 ] ] | [ML-3] |
Our postulated expression becomes
![[L3T- 1] = k[L]a[M L -1T-2]b[M L- 3]c](../DimensionalAnalysis/dimensionalLecture17x.gif) Now the dimensions of mass [M] have to balance on both sides of this expression, so the exponents have to
satisfy
Now the dimensions of mass [M] have to balance on both sides of this expression, so the exponents have to
satisfy
 Also, the dimensions of [L] and [T] must balance. For this to be the case
Also, the dimensions of [L] and [T] must balance. For this to be the case
| 3 | = a - b - 3c for [L] | |
|
| - 1 | = -2b for [T] | | |
By writing this out like this, we have produced 3 simultaneous equations for the 3 unknowns a, b and c, from
which we can see
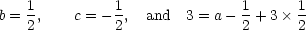 so a = 2. Putting these values for the exponents back into the original expression (1),
so a = 2. Putting these values for the exponents back into the original expression (1),
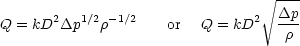 | (2) |
Again, k is a dimensionless constant whose value has to be determined via some other method typically
experimentally. Knowing that the relationship has to be of the form (2), we could design an experiment where,
for instance, Q is measured for different values of 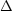 p, and a plot of Q versus
p, and a plot of Q versus 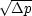 would give a straight line
with slope kD2/
would give a straight line
with slope kD2/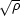 .
.
3.2 More variables
What happens if we realise that there are more variables in the problem we are considering? The previous
example assumed the flow to be ideal, i.e. the viscosity is zero. For a real fluid, Q may well depend on the
viscosity. In this case equation (1) would have to be
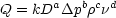 i.e. (inserting the appropriate dimensions)
i.e. (inserting the appropriate dimensions)
![[L3T -1] = k[L]a[M L-1T- 2]b[M L -3]c[L2T-1]d](../DimensionalAnalysis/dimensionalLecture24x.gif) Equating dimensions gives
Equating dimensions gives
| [M] : | 0 | = b + c | | | |
|
| [L] : | 3 | = a - b - 3c + 2d | | | |
|
| [T] : | - 1 | = -2b - d | | | | |
Now we have 3 equations and 4 unknowns, so there is no unique solution. The best we can hope for will be to
express everything in terms of one of the exponents, say b :
| c | = -b | |
|
| d | = 1 - 2b | |
|
| 3 | = a - b + 3b + (2 - 4b) 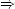 a = 1 + 2b a = 1 + 2b | | |
In this case the equation will become
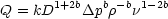 This could be rearanged into the form
This could be rearanged into the form
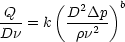 We note that both
We note that both
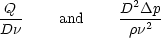 are dimensionless combinations of the variables. In fact, since
are dimensionless combinations of the variables. In fact, since
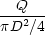 is the mean velocity, Q/D
is the mean velocity, Q/D is a Reynolds number for the problem.
is a Reynolds number for the problem.
3.3 Summary
- In fluid mechanics, generally we deal with 3 base dimensions, M, L, T. If a problem involves 4 variables A,
B, C, D, we can relate these as an equation of the form
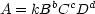 and determine the coefficients b, c, d
and determine the coefficients b, c, d
- If there are more than 4 variables - say E, F, then we cannot uniquely determine their coefficients. The
best we can hope for is to find groups of variables that are themselves dimensionless. There is a general
method for doing this called the Buckingham
 theorem, (section 4).
theorem, (section 4).
- There are exceptions to both of these statements. For example, if there are 4 dimensional quantities
involved - maybe a heat transfer problem involving the dimension of temperature [
 ] - we can determine
a relation between up to 5 different variables.
] - we can determine
a relation between up to 5 different variables.
![]() p. It seems
plausible that Q might also depend on the density of the fluid
p. It seems
plausible that Q might also depend on the density of the fluid ![]() , so we look for a relationship of the
form
, so we look for a relationship of the
form