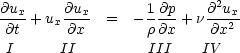5 Similarity

It might be thought that the Buckingham technique of finding dimensionless groups would be less powerful than one that produces the full relation. In fact this is not really the case. Dimensionless groups are enormously useful in fluid dynamics, because of the idea of dynamic similarity.

If we want to perform an experiment, say measuring the drag force on an aircraft, we often build a scale model of the aircraft and place it in an appropriate flow. Clearly in this case the model should be an exact scale model. If it is, then we say the two flows (the real aircraft and the model) posess geometric similarity.

Dynamic similarity occurs if the forces acting on equivalent bodies in the two flows are always in the same ratios. For the real and model aircraft example, this means that the ratio

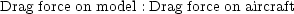Drag force on model : Drag force on aircraft

is the same as the ratio

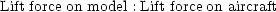Lift force on model : Lift force on aircraft

In this particular case, dynamic similarity occurs when the Reynolds numbers are the same for the aircraft and for the model. Under these circumstances the dimensionless lift and drag coefficients C_L, C_D will be the same, and so we can use experimental results from the model to predict the forces acting on the whole aircraft. For any type of flow we can construct appropriate dimensionless groups, and if the values of the groups are the same for two flows then the two flows are dynamically similar.

5.1 Particular groups

Different dimensionless groups are appropriate for different flow problems, and their identification is an important part of understanding the flow regimes. The groups are always constructed from characteristic scales in the problem, for instance a characteristic length L or a characteristic speed V . Some important dimensionless groups include

Reynolds :: The Reynolds number 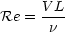$Re = VL- n$ is a measure of the ratio of the inertia of the fluid to the viscous forces. Its value is indicative of whether the fluid is laminar or turbulent.
Froude :: The Froude number 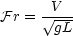$V~ -V- Fr = gL$ is a measure of the ratio of inertia to gravitational forces, and is important for free surface flows. In open channel flow, it indicates whether flow is sub-critical or super-critical : it is also important for modelling ships.
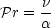Prandtl :: The Prandtl number is important in convective heat transfer. It is the ratio of kinematic viscosity to thermal diffusivity $n- Pr = a$ and the product Re × Pr is a measure of the ratio of heat transfer by convection to heat transfer by conduction.
Mach :: The Mach number is the ratio of a characteristic flow speed V to the speed of sound in the fluid c 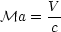$V Ma = c-$ For Ma « 1 the fluid can be considered to be incompressible, whilst for Ma > 1 the flow is supersonic.

5.2 Derivation (simple)

There are several routes by which these dimensionless groups can be extracted from the problem. The Buckingham method is one way. However the Froude and Reynolds numbers can be derived via a simple consideration of the inertia and other forces acting. The Froude number is the ratio of inertial to gravitational effects on the flow. The inertia of an element of the fluid is ma, with m the mass of the element : since the accelleration a is dimensionally a characteristic velocity V divided by a characteristic time T then this can be written

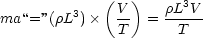( ) 3 ma “=”(rL3)× V- = rL-V- T T

Meanwhile the gravitational force on an element is F_g =

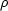L³g, with g the accelleration due to gravity. Now if flows A and B are dynamically similar, then the ratio of the inertial forces has to be the same as the ratio of the gravitational forces :

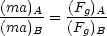(ma)A- = (Fg)A- (ma)B (Fg)B

In other words

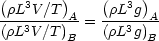(rL3V/T ) (rL3g) ---3-----A = ---3--A- (rL V/T )B (rL g)B

Rearanging this

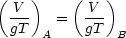( V ) ( V ) --- = --- gT A gT B

Finally, in dimensional terms V “=”L/T, so we can eliminate the characteristic time T

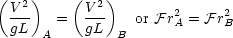( 2 ) ( 2) V-- = V-- or Fr2A = Fr2B gL A gL B

This is a slightly non-rigorous derivation, hence the “=” signs, however it does bring out the physical basis of the Froude number. A similar approach can be used to derive the Reynolds number.

5.3 Derivation (advanced)

An alternative approach to deriving the Reynolds number is to look at the momentum equation. In 1-d this is

@ux- @ux- 1@p- @2ux- @t + ux @x = - r@x + n@x2 I II III IV

Consider term I first. u_x has dimensions of velocity, so if we have a characteristic velocity V in the problem, we can work in terms of a dimensionless quantity, u^* = u_x/V . However the time derivative has dimensions of time. If we also have a characteristic time scale T in the problem, then we can multiply the first term by T/V :

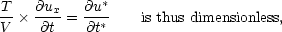-T @ux- @u*- V × @t = @t* is thus dimensionless,

with t^* a dimensionless time variable. So what happens if we multiply the other terms by this factor T/V ?

Term II.: This is straightforward : since V “=”L/T, 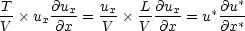$T- @ux- ux- L-@ux- *@u*- V × ux@x = V × V @x = u @x*$ with x^* a dimensionless position variable.
Term III: is less obvious, but 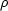V ² has dimensions of pressure, so 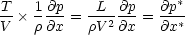$T 1@p L @p @p* V-× r@x-= rV-2@x-= @x*-$ where p^* = p/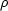V ².
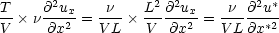
Term IV.: We can write this as $T- ×n @2ux-= -n-× L2-@2ux-= -n-@2u* V @x2 VL V @x2 V L@x*2$

But we have generated a term

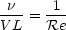n 1 VL-= Re-

out of this! Thus, if we write the whole equation out in these non-dimensional variables, it becomes

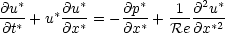
@u*- *@u*- @p*- -1-@2u* @t* + u @x* = -@x* + Re @x*2

So what have we achieved by doing this? Well, consider this : if we take our real and model aircraft, and draw plans, measuring distances using (say) the width of the fusilage as our basic unit, the numbers will come out the same (geometric similarity). Hence, for both cases the wingspan is 25 units, the length 21 units, etc. Using these dimensionless variables u^*, x^* etc. terms I, II and III will be the same. Term IV contains all the information about the real size of the aircraft, all in the term 1/Re. So if the Reynolds number is the same for both cases, the momentum equation will be identical - and so must be the solutions.

[next] [prev] [prev-tail] [front] [up]