IV.2 Turbulence
Turbulence is virtually impossible to avoid in fluid flow problems, and its modelling is one of
the most significant challenges in CFD. To understand why, let us estimate the computational
cost of simulating turbulence. A turbulent flow is comprised of eddies on scales from the
size of the domain down to a size called the Kolmogorov scale 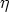 which is related
to the viscosity of the fluid
which is related
to the viscosity of the fluid  and the rate of dissipation of the turbulent energy
and the rate of dissipation of the turbulent energy

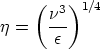 Of course, such a flow obeys the NSE at all scales, and so we could simulate the flow. We
would need to construct a mesh fine enough to resolve all these length scales. For the flow
around a car, say at Re = 500, 000 (equivalent to the car travelling at about 20 km/hr),
Of course, such a flow obeys the NSE at all scales, and so we could simulate the flow. We
would need to construct a mesh fine enough to resolve all these length scales. For the flow
around a car, say at Re = 500, 000 (equivalent to the car travelling at about 20 km/hr),
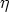 ~ 1mm, and so we would need
~ 1mm, and so we would need
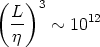 cells, where L is a characteristic dimension of the car. This is well beyond the capacity of any
existing computer. In general, the cost of DNS varies with Reynolds number as Re9/4, so the
more turbulent the flow the more expensive the simulation. We need to find some way to
reduce the complexity of this calculation.
cells, where L is a characteristic dimension of the car. This is well beyond the capacity of any
existing computer. In general, the cost of DNS varies with Reynolds number as Re9/4, so the
more turbulent the flow the more expensive the simulation. We need to find some way to
reduce the complexity of this calculation.
The way to do this is to split the flow into two components : an average component, and
fluctuations around that average. The average component will depend on the exact problem
being solved (geometry, boundary conditions etc) and so will be explicitly simulated, whilst
the fluctuating components will be labelled ‘turbulence’, and we will replace these components
with a simple model based on our knowledge of the properties of turbulence in general. For
instance, the velocity can be written as
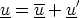 This averaging could be a time average, for example :
This averaging could be a time average, for example :
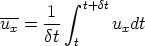 for the ux component of velocity. Note that
for the ux component of velocity. Note that
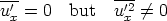 Of course,
Of course,  u2 is the expression for kinetic energy, so
u2 is the expression for kinetic energy, so 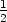 ux'2 is going to be related to the kinetic
energy of the turbulent component of the flow.
ux'2 is going to be related to the kinetic
energy of the turbulent component of the flow.
If we apply this averaging to the momentum equation
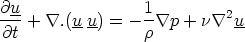 we end up with a very similar equation called the Reynolds equation :
we end up with a very similar equation called the Reynolds equation :
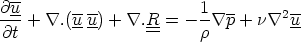 containing an additional term
containing an additional term  .R. R is called the Reynolds stress, and it represents
the effect of the fluctuating components on the mean flow. We can write it out in
full :
.R. R is called the Reynolds stress, and it represents
the effect of the fluctuating components on the mean flow. We can write it out in
full :
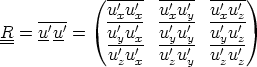 Other than this additional term, the Reynolds equation is the same as the the original
momentum equation, and can be solved in exactly the same way. Because it is an equation for
the mean velocity, ignoring turbulent effects, the complexity of the flow that it describes is
much less, and so the cost of the solution is also much less.
Other than this additional term, the Reynolds equation is the same as the the original
momentum equation, and can be solved in exactly the same way. Because it is an equation for
the mean velocity, ignoring turbulent effects, the complexity of the flow that it describes is
much less, and so the cost of the solution is also much less.
However we have a problem. In the original case we had 4 equations for 4 unknowns p, 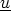 .
Now we have 4 equations for more than 4 unknowns p,
.
Now we have 4 equations for more than 4 unknowns p, 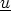 ,
, 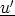 . This is termed the closure problem
- we need to find an expression for R in terms of p,
. This is termed the closure problem
- we need to find an expression for R in terms of p, 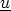 somehow.
somehow.
Turbulence is often seen to have a diffusive effect. For instance, perfume in still air diffuses
away from its source. In turbulent air, the same effect occurs, but the mixing is much faster.
Thus we will model the turbulence here as a diffusive term
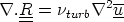 where
where  turb is the turbulent viscosity of the flow. This is known as the eddy viscosity, or
Boussinesq approximation. If 1 velocity scale vt and 1 length scale lt can be used to describe
the effects of turbulence, then
turb is the turbulent viscosity of the flow. This is known as the eddy viscosity, or
Boussinesq approximation. If 1 velocity scale vt and 1 length scale lt can be used to describe
the effects of turbulence, then
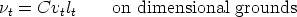 The turbulent kinetic energy gives a velocity scale
The turbulent kinetic energy gives a velocity scale
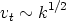 The turbulent energy will also be dissipated continuously via viscous processes at the smallest
scales (around the Kolmogorov scale). We can call the rate at which this happens the turbulent
dissipation rate
The turbulent energy will also be dissipated continuously via viscous processes at the smallest
scales (around the Kolmogorov scale). We can call the rate at which this happens the turbulent
dissipation rate  .
.  has dimensions
has dimensions ![[L2T -3]](notes418x.gif) , and so units m2s-3. From this we can construct a
length scale
, and so units m2s-3. From this we can construct a
length scale
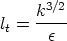 Using all of this we have an expression for the turbulent viscosity
Using all of this we have an expression for the turbulent viscosity
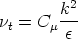 Thus, if we can evaluate k and
Thus, if we can evaluate k and  , we have a model for
, we have a model for 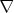 .R and we can solve for the
flow.
.R and we can solve for the
flow.
![]() which is related
to the viscosity of the fluid
which is related
to the viscosity of the fluid ![]() and the rate of dissipation of the turbulent energy
and the rate of dissipation of the turbulent energy
![]()
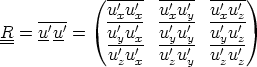
![]() .
Now we have 4 equations for more than 4 unknowns p,
.
Now we have 4 equations for more than 4 unknowns p, ![]() ,
, ![]() . This is termed the closure problem
- we need to find an expression for R in terms of p,
. This is termed the closure problem
- we need to find an expression for R in terms of p, ![]() somehow.
somehow.