4 Runge-Kutta solution
In order to solve O.D.E’s such as the Blasius equation (5) we often need to resort to computer methods. Let us
start by thinking about what an O.D.E actually represents. A first order O.D.E is a statement that the gradient
of y, dy/dx, takes some value or function. We can write this as
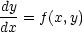 Given a particular starting point - some value of y corresponding to a given value of x - this
equation specifies a particular curve in the x - y plane. A typical such solution is shown in figure
3.
Given a particular starting point - some value of y corresponding to a given value of x - this
equation specifies a particular curve in the x - y plane. A typical such solution is shown in figure
3.
We could trace the curve defined by this O.D.E - i.e. solve the equation - by starting at this point and
tracing forwards/backwards in steps of size h
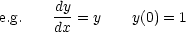 In fact this is the basis for all numerical methods for solving O.D.E’s. Used like this, it is referred to as Euler’s
method. Symbolically, we are writing the derivative as
In fact this is the basis for all numerical methods for solving O.D.E’s. Used like this, it is referred to as Euler’s
method. Symbolically, we are writing the derivative as
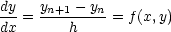 which we can rewrite to find point yn+1 from point yn
which we can rewrite to find point yn+1 from point yn
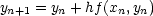 | (6) |
Obviously the smaller the step h being used, the more accurate the resulting solution will be. In fact, a more
exact analysis shows that equation 6 is missing a term of the form h2. We therefore say that the scheme is first
order accurate. However using smaller steps h also increases the computational cost of the calculation, and it
may be better to try to find more accurate schemes. It is possible to combine Euler steps of various sizes in a
scheme in such a way as to produce a more accurate final scheme. The Runge-Kutta family of numerical
schemes is constructed in this way. To solve the Blasius equation we will make use of the 4th order
Runge-Kutta method, so called because it is 4th order accurate (the missing terms in the scheme are of the
form h5).
The 4th order Runge-Kutta method is available in MathCad in the form of a function call rkfixed. You
will make use of this in Problem Sheet 3153-1 to solve the Blasius problem.
Of course, in this case we can solve the problem analytically. The solution is
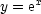
4.1 Higher order O.D.E’s
The Blasius equation is a 3rd order O.D.E, and the discussion above talked about 1st order O.D.E’s. It is
possible to use Runge-Kutta for higher order O.D.E’s, but we must first manipulate the equation we want to
solve. For instance, suppose we want to solve the equation
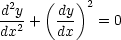 For this equation, define a new variable
For this equation, define a new variable
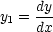 Using this variable
Using this variable
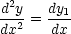 and we can write the 2nd order ODE as 2 1st order equations :
and we can write the 2nd order ODE as 2 1st order equations :
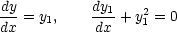 If we define a vector
If we define a vector
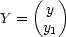 then we could write these as
then we could write these as
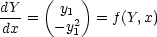 which is in the same form as before - a 1st order O.D.E, but involving a vector of y values.
which is in the same form as before - a 1st order O.D.E, but involving a vector of y values.
For the Blasius equation,
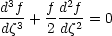 if we write
if we write
 we solve the equations Of course, we still need to find the boundary conditions in order to be able to solve these equations. We note
that at the plate y = 0 the velocity is zero ux = 0, whilst a long way from the plate the flow has to match the
undisturbed flow ux
we solve the equations Of course, we still need to find the boundary conditions in order to be able to solve these equations. We note
that at the plate y = 0 the velocity is zero ux = 0, whilst a long way from the plate the flow has to match the
undisturbed flow ux  U
U :
:
-
Boundary 1
- At the plate y = 0, i.e.
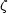 = 0, ux = 0 i.e. f' = 0, f = 0.
= 0, ux = 0 i.e. f' = 0, f = 0.
-
Boundary 2
- A long way from the plate, i.e. y

 , i.e.
, i.e. 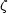

 , ux
, ux  U
U , i.e. f'
, i.e. f'  1
1
This gives us a sufficient number of boundary conditions, but they are in two different locations. The rkfixed
routine in MathCad requires you to specify values for Y 0, Y 1 and Y 2 for a specific value of X, and will return
the solution for other values of X starting at this point. The only way to find the solution in this case is to use
a shooting method. We know that at X = 0, Y 0 = Y 1 = 0. Guess a value of Y 2 at this point and then adjust it
until the second boundary condition is satisfied.