I.4 FV for transport equation
To demonstrate this, let us solve the following problem : water flowing in a river is
contaminated by a chemical leak. We want to determine where the chemical has reached after
a given time t. The channel is shown in figure 1. The flow is uniform throughout the channel
with speed u at all points. The concentration q of the contaminant is described by the
following equation
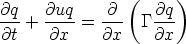 | (I.4) |
which is known as the 1-d transport equation. As we will see this is a very common equation in
CFD.
Figure 1 also shows the mesh to be used. We have split the channel up into a series of cells
of volume 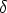 V = A
V = A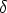 x, where A is the area of the faces between the boxes. To apply the FV
method, we integrate (I.4) over the volume of the cell. This will be a triple integral dV over
the volume
x, where A is the area of the faces between the boxes. To apply the FV
method, we integrate (I.4) over the volume of the cell. This will be a triple integral dV over
the volume 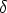 V .
V .
The first term is easy, since we can swap the order of the integral and the time
derivative :
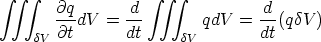 In the last step, we have assumed that the value of q is uniform over the whole cell, so the
value of the integral is the value of q (stored at the cell centre multiplied by the volume of the
cell.
In the last step, we have assumed that the value of q is uniform over the whole cell, so the
value of the integral is the value of q (stored at the cell centre multiplied by the volume of the
cell.
The second term is more difficult. However, in this case the volume dV = Adx, and
so
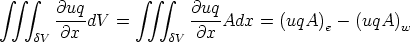 These two terms are now being evaluated on the boundary face between the cells. It is
conventional to refer to the cells using compass directions : we consider a particular cell P , its
neighbours W and E, and the cell faces separating the cells as w and e respectively. However
we do not know the value of the variables on w and e, just the values stored at the cell centres
W , P and E. We need to interpolate between these values. One possibility would be
to take the value from the upstream cell. In this case the flow is W
These two terms are now being evaluated on the boundary face between the cells. It is
conventional to refer to the cells using compass directions : we consider a particular cell P , its
neighbours W and E, and the cell faces separating the cells as w and e respectively. However
we do not know the value of the variables on w and e, just the values stored at the cell centres
W , P and E. We need to interpolate between these values. One possibility would be
to take the value from the upstream cell. In this case the flow is W  E, so this
means
E, so this
means
 This is referred to as upwind differencing. Alternatively we could average between the two cell
centre values :
This is referred to as upwind differencing. Alternatively we could average between the two cell
centre values :
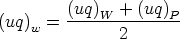 and similarly for
and similarly for 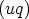 e. This is known as central differencing. (Note that the area
A is the same throughout, and so has been factored out. This is not always the
case).
e. This is known as central differencing. (Note that the area
A is the same throughout, and so has been factored out. This is not always the
case).
The term on the rhs. representing diffusion can be treated similarly :
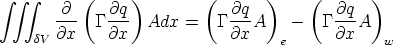 Once again, we can express each of these terms in terms of the cell centre values, for
example :
Once again, we can express each of these terms in terms of the cell centre values, for
example :
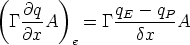
Thus far we can write our discretised equations as
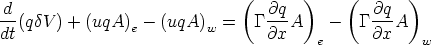 Rearanging a bit and using central differencing to interpolate, we get
Rearanging a bit and using central differencing to interpolate, we get
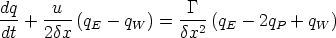 This is a discretised equation for a single cell. If we number the cells i = 0...N, then we have a
set of difference equations for the derivative
This is a discretised equation for a single cell. If we number the cells i = 0...N, then we have a
set of difference equations for the derivative 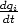 :
:
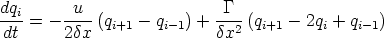 | (I.5) |
![]() V = A
V = A![]() x, where A is the area of the faces between the boxes. To apply the FV
method, we integrate (I.4) over the volume of the cell. This will be a triple integral dV over
the volume
x, where A is the area of the faces between the boxes. To apply the FV
method, we integrate (I.4) over the volume of the cell. This will be a triple integral dV over
the volume ![]() V .
V .