2 Simple uses

At the most basic level, dimensional analysis can be used to convert from one set of units to another, and to check the validity of equations. In both cases we are using the fact that no matter what units we are using, each term in any equation has to have the same overall dimensions.

2.1 Converting units

First, a cautionary tale. On September 23rd 1999, NASA’s Mars Climate Orbiter crashed whilst trying to execute a difficult breaking manouver to arrive at Mars, and a spacecraft costing $360 million was lost. Investigations after the event showed that the subcontractors building the probe used Imperial units (pounds force for thruster impulse) whilst NASA was using metric units of Newtons, and the conversion factor between the two systems had been neglected.

Let us see if we can convert from a force in Imperial units (FPS technical) to a force in metric units. First off, the quantity force must always have the same dimension :

Force [F ] has dimensions [M LT -2]

In the FPS system, force is measured in pounds force, which is the force necessary to accellerate a mass of 1 slug (the FPS unit of mass) 1 ft/s². The conversion factors are given in the following table

Quantity	FPS	SI	Ratio (SI/FPS)

Mass	Slug	kg	14.60
Length	foot (ft)	m	0.3048
Time	seconds (s)	s	1

If we have a force of X lbf = X slug ft/s², then we can write

2 ( )( )( - 2) F = X slug ft/s2 = X slug-ft/s-kg m/s2 = X slug- -ft s-- kg m/s2 kg m/s2 kg m s- 2

Inserting the ratios (kg in 1 slug, m in 1 ft),

F = X 14.60 × 0.3048× 12 kg m/s2 = X × 4.45 kg m/s2

So the conversion factor to go from FPS to SI units of force is 4.45.

2.2 Checking equations

A second useful application of this is to check equations. A valid equation has to be dimensionally homogeneous, i.e. all the terms in the equation have to have the same dimensions. By ‘term’ here we mean groups of variables multiplied together or divided. As an example, the momentum equation in 1-d can be written as

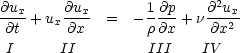
@ux- @ux- 1@p- @2ux- @t + ux @x = - r@x + n@x2 I II III IV

Here,

Term I: has dimensions $-1 [ux]-= [LT---]= [LT -2] [t] [T]$
Term II: has dimensions $[LT -1] [LT -1]------= [LT- 2] [L]$
Term III: has dimensions $---1---[M-L-1T--2] -2 [M L-3] [L] = [LT ]$
Term IV: is the most complex. The kinematic viscosity, , has units m2 s-1, so that has dimensions [L²T^-1]. Thus the term itself has dimensions $[L2T-1][LT-1] = [LT -2] [L2]$

In other words, all the terms in this equation have the same dimensions, so we conclude that there is nothing wrong here. Of course, the momentum equation is a well-known one, but we might be dealing with a less recognisable equation. We can use this technique to check equations, or to work out the dimensions (and then units) for unknown variables in an equation.

[next] [prev] [prev-tail] [front] [up]