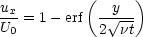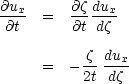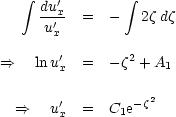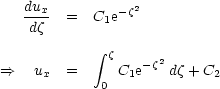2 Impulsively started plate

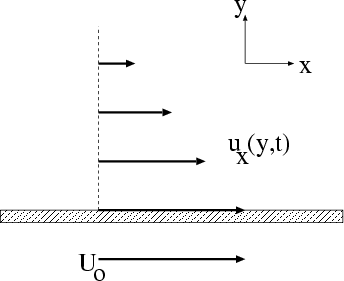
We will start by looking at a simple laminar boundary layer, formed when a plate starts moving in a stationary fluid. This is referred to as an impulsively moving plate. Initially the plate and the fluid around it are stationary. At time t = 0 the plate begins to move sideways (see figure 1) with speed U₀. This will have an effect on the fluid immediately surrounding the plate, which will start moving with the same speed. This will then influence fluid a bit further out, which will begin to move (a bit slower). This in turn will influence the next layer of fluid, which will start to move. The important point to notice is that it takes time for each layer of fluid to influence the next one out. Hence we expect a moving layer of fluid to develop around the plate - the boundary layer - which will grow outwards as time progresses.

Figure 1:

Impulsively started plate

If this is the case - i.e. there is no flow in the y direction, and no variation in the flow in the x direction (the plate is assumed to be infinitely long).

The momentum equation in 2d cartesian coordinates is

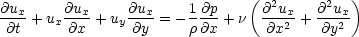@ux @ux @ux 1 @p (@2ux @2ux) @t-+ ux @x-+ uy @y-= - r @x + n -@x2-+ -@y2-

For this case we would expect to get a solution for this problem of the form u_x(y, t) - i.e. there is no flow in the y direction, and no variation in the flow in the x direction (the plate is assumed to be infinitely long). This implies

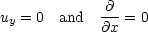@ uy = 0 and @x-= 0

and so the momentum equation reduces to

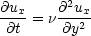@ux- @2ux- @t = n @y2

(1)

However this is still a partial differential equation (P.D.E). To solve it we need to reduce it to an ordinary differential equation (O.D.E). We can do this via a technique known as Combination of Variables. Let us assume that u_x is a function of a single variable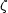

ux = ux(z) z = z(x,t)

where

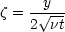z = -y V~ --- 2 nt

is a dimensionless variable. (Note that this is another example of the use of dimensional analysis in problem solving - y, t and

are the only dimensional parameters in the problem, and so we can see that the solution must depend on some dimensionless combination of these parameters). Using the chain rule of differentiation we can show that

@ux- @zdux- @t = @t dz = --z dux- 2t dz

and

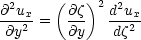@2ux (@z )2 d2ux -@y2-= @y- dz2-

so equation 1 becomes

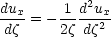dux 1 d2ux -dz-= - 2z-dz2

(2)

- a second order O.D.E, which we can solve.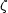

here is a variable which encapsulates both spatial and temporal variation. Thus as time progresses (t increases) the solution for a given value of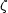

corresponds to a physical point further and further away from the plate (y increases). This corresponds to our notion that the boundary layer is growing with time. The actual solution of equation 2 is fairly straightforward. If we write

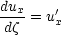dux- ' dz = ux

it becomes

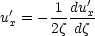' -1 du'x- ux = -2z dz

a 1st order O.D.E, which is separable :

integral ' integral dux- = - 2z dz u'x ' 2 ==> lnux = -z + A1 ==> u'x = C1e-z2

i.e.

dux- = C e-z2 dz 1 integral z ==> ux = C1e-z2 dz + C2 0

Finally we need to evaluate C₁, C₂, for which we need to know the boundary conditions.

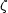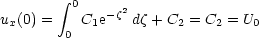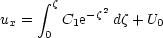
B.C.1: At y = 0, i.e. at = 0, u_x(0) = U₀, so $integral 0 2 ux(0) = C1e-z dz + C2 = C2 = U0 0$ so $integral z 2 ux = C1e-z dz + U0 0$
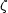
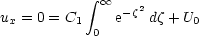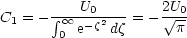
B.C.2: As y , i.e. , u_x 0 In this case $integral oo ux = 0 = C1 e-z2 dz + U0 0$ Rearanging this we find $U 2U C1 = - integral - oo -0-z2-- = - V~ -0 0 e dz p$

and so

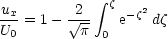integral ux-= 1- V~ 2- z e- z2 dz U0 p 0

Note that the integral

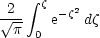2 integral z -z2 V~ p e dz 0

is a mathematical function called the Error Function erf(

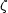), with tables of values available. The solution for this case is thus often written in the form

ux ( y ) U0-= 1- erf 2 V~ nt

[next] [prev] [prev-tail] [front] [up]