|
Turbulence Models |
||||||||||||||
| Home
Page
Section 1 - The Problem Section 2 - The Tools Section 3 - Results Section 4 - Previous Work
|
k-ε model The k-ε model is the most commonly used of all the turbulence models. It is classified as a two equation model. This denotes the fact that the transport equation is solved for two turbulent quantities k and ε. Within the model the properties k and ε are defined through two transport equations (1) and (2).
k-ω model The k-ω model is the second most widely used turbulence model and is also classified as a two equation model. This model is very similar to the k-ε model and uses the same definition for k as previously outlined (1). However the k-ω model differs in its selection of a second variable for characterising turbulent behaviour. The equation for ω is defined by the following equation (3).
Reynolds Stress Reynolds Stress models solve for individual Reynolds stresses and for the turbulent dissipation ε. The Reynolds Stress model assumes that the factors within it contain no dependence on the Reynolds number of the flow. However it should be noted that this is not always true especially at moderate Reynolds numbers. The central concept of the Reynolds stress model is that the stress tensor Rij is determined locally within the cell. This assumption provides the main weakness to the Reynolds stress model in that it often disregards long range effects caused by walls and other objects within the flow.
Strengths and Weaknesses
Choice k-ε model because k-ω model offers no advantage and Reynolds Stress would be too computationally demanding for a large 3-D case. |
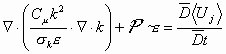 (1)
(1)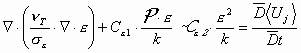 (2)
(2)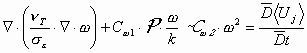 (3)
(3)