II.2 3d Transport Equations using FV method
The generic transport equation was introduced in the last lecture. This can be written in
vector notation as
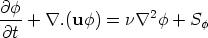 | (II.1) |
To apply the FV method to this equation, we divide the region of interest up into cells, and
integrate this equation over the volume of each cell in turn.
The first term in the equation becomes
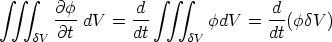 if we assume that
if we assume that 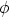 is uniform over the cell - valid if the cell is small enough, which is what we
want. We assume that
is uniform over the cell - valid if the cell is small enough, which is what we
want. We assume that 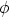 is associated with the cell centre, and that we can express this as the
difference in the value of
is associated with the cell centre, and that we can express this as the
difference in the value of 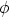 at two times
at two times
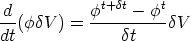
The second term
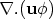 represents convection of fluid into and out of the cell. Integrating this is complicated, but
produces a simple answer - this term can be represented as the flux of
represents convection of fluid into and out of the cell. Integrating this is complicated, but
produces a simple answer - this term can be represented as the flux of 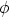 across the cell
faces
across the cell
faces
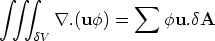 Here the faces
Here the faces 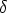
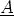 have been written as vector areas - giving the direction in which
the surface points as well as its size. If for example the problem is 1d, with a flow
(and a mesh) orientated in the x direction as in the last lecture, then this term
becomes
have been written as vector areas - giving the direction in which
the surface points as well as its size. If for example the problem is 1d, with a flow
(and a mesh) orientated in the x direction as in the last lecture, then this term
becomes
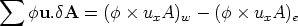 Of course, we still need to evaluate the values of these variables on the face centres.
Of course, we still need to evaluate the values of these variables on the face centres.
A CFD mesh is sometimes described as either colocated or staggered. If the mesh is
colocated, then all the variables are stored at the cell centres, and we need to find some way of
interpolating between the cell centres to get the value of the flux at the face. If the
mesh is staggered, then some variables are stored at the face locations. However
this is simply a matter of storage - at some stage the code needs to perform an
interpolation.
There are two simple ways of interpolating to get the face value from the cell centre
values :
- Take the value from the upwind cell centre - upwind differencing
- Take an average of the two cell centres - central differencing
These are illustrated in figure 4.
Although strictly speaking these are interpolations between cell centred values, they are
exactly equivalent to the upwind and central differencing methods used in FD, and so are
referred to as differencing schemes. They are of course approximations. Upwind
differencing produces an error involving 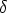 x2 and higher, and so is said to be 1st order
accurate. Central differencing has an error involving
x2 and higher, and so is said to be 1st order
accurate. Central differencing has an error involving 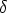 x3, so is 2nd order accurate.
As important as the order of the error is the type of effect it induces. This is best
explored by looking at what the scheme does to a step function such as the one
below.
x3, so is 2nd order accurate.
As important as the order of the error is the type of effect it induces. This is best
explored by looking at what the scheme does to a step function such as the one
below.
- Upwind differencing introduces numerical viscosity. The error is equivalent to
increasing the viscosity of the fluid, which results in the step being smeared out.
This can lead to structures such as shocks being lost from the solution.
- Central differencing introduces phase errors. The solution ‘rings’, leading to
oscillations before and after the step. This can lead to numerical instability in the
solution
More sophisticated schemes are also used, either to increase the order of accuracy of the
differencing scheme (e.g. up to 4th order) or to merge features of the upwind and central
differencing schemes. For example a number of schemes attempt to blend these two to provide
a scheme which introduces the minimum numerical viscosity necessary to stabilise
features such as shocks, but without smearing them out more than is absolutely
necessary.
These techniques can also be utilised to evaluate the diffusion term
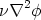 The source term is straightforward to express. We assume that the value of S
The source term is straightforward to express. We assume that the value of S is uniform over
the cell, and so
is uniform over
the cell, and so
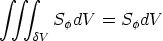 If all of these expressions are recombined, the result is a difference equation linking the values
of
If all of these expressions are recombined, the result is a difference equation linking the values
of 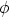 at the cell centres at time t +
at the cell centres at time t + 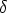 t to the values at time t. Depending on exactly how this is
done, the result is either an explicit scheme (the equation can be rearanged directly to give
t to the values at time t. Depending on exactly how this is
done, the result is either an explicit scheme (the equation can be rearanged directly to give
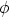 t+
t+ t in terms of values already known at time t) or an implicit scheme, which can be written
as
t in terms of values already known at time t) or an implicit scheme, which can be written
as
![M[ft+dt] = Q](notes216x.gif)
![]() x2 and higher, and so is said to be 1st order
accurate. Central differencing has an error involving
x2 and higher, and so is said to be 1st order
accurate. Central differencing has an error involving ![]() x3, so is 2nd order accurate.
As important as the order of the error is the type of effect it induces. This is best
explored by looking at what the scheme does to a step function such as the one
below.
x3, so is 2nd order accurate.
As important as the order of the error is the type of effect it induces. This is best
explored by looking at what the scheme does to a step function such as the one
below.